Hello all we know that as a besic need we should know about the Kirchoff Laws
KIRCHHOFF’S LAWS
Ohm’s law by itself is not sufficient to analyze circuits. However, when
it is coupled with Kirchhoff’s two laws, we have a sufficient, powerful
set of tools for analyzing a large variety of electric circuits. Kirchhoff’s
laws were first introduced in 1847 by the German physicist Gustav Robert
Kirchhoff (1824–1887). These laws are formally known as Kirchhoff’s
current law (KCL) and Kirchhoff’s voltage law (KVL).
Kirchhoff’s first law is based on the law of conservation of charge,
which requires that the algebraic sum of charges within a system cannot
change
Kirchoff's Current Law (KCL) :
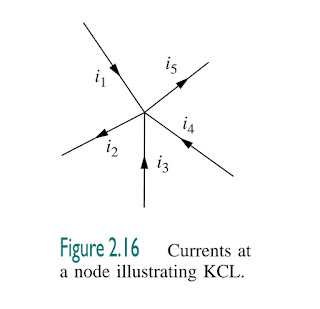
Kirchhoff’s current law (KCL) states that the algebraic sum of currents entering
a node (or a closed boundary) is zero
a node illustrating KCL. Consider the node in Fig. 2.16. Applying KCL gives
i1 + (−i2) + i3 + i4 + (−i5) = 0
since currents i1, i3, and i4 are entering the node, while currents i2 and
i5 are leaving it. By rearranging the terms, we get
i1 + i3 + i4 = i2 + i5
Kirchoff's Voltage Law (KVL) :
Kirchhoff’s voltage law (KVL) states that the algebraic sum of all voltages
around a closed path(or loop) is zero.
o illustrate KVL, consider the circuit The sign on each voltage is the polarity of the terminal encountered first as we travel around the loop. We can start with any branch and go around the loop either clockwise or counterclockwise. Suppose we start with the voltage source and go clockwise around the loop as shown; then voltages would
be
−v1, +v2, +v3, −v4, and +v5, in that order.
For example, as we reach
branch 3, the positive terminal is met first; hence we have +v3. For branch
4, we reach the negative terminal first; hence, −v4. Thus, KVL yields
−v1 + v2 + v3 − v4 + v5 = 0
Rearranging terms gives
v2 + v3 + v5 = v1 + v4
which may be interpreted as
Sum of voltage drops = Sum of voltage rises
Apply Kvl To above Figure And Find Answer......
Comment Your Answer And Comment If you have any doubt and keep supporting us
KIRCHHOFF’S LAWS
Ohm’s law by itself is not sufficient to analyze circuits. However, when
it is coupled with Kirchhoff’s two laws, we have a sufficient, powerful
set of tools for analyzing a large variety of electric circuits. Kirchhoff’s
laws were first introduced in 1847 by the German physicist Gustav Robert
Kirchhoff (1824–1887). These laws are formally known as Kirchhoff’s
current law (KCL) and Kirchhoff’s voltage law (KVL).
Kirchhoff’s first law is based on the law of conservation of charge,
which requires that the algebraic sum of charges within a system cannot
change
Kirchoff's Current Law (KCL) :
Kirchhoff’s current law (KCL) states that the algebraic sum of currents entering
a node (or a closed boundary) is zero
a node illustrating KCL. Consider the node in Fig. 2.16. Applying KCL gives
i1 + (−i2) + i3 + i4 + (−i5) = 0
since currents i1, i3, and i4 are entering the node, while currents i2 and
i5 are leaving it. By rearranging the terms, we get
i1 + i3 + i4 = i2 + i5
Kirchoff's Voltage Law (KVL) :
Kirchhoff’s voltage law (KVL) states that the algebraic sum of all voltages
around a closed path(or loop) is zero.
be
−v1, +v2, +v3, −v4, and +v5, in that order.
For example, as we reach
branch 3, the positive terminal is met first; hence we have +v3. For branch
4, we reach the negative terminal first; hence, −v4. Thus, KVL yields
−v1 + v2 + v3 − v4 + v5 = 0
Rearranging terms gives
v2 + v3 + v5 = v1 + v4
which may be interpreted as
Sum of voltage drops = Sum of voltage rises
Apply Kvl To above Figure And Find Answer......
Comment Your Answer And Comment If you have any doubt and keep supporting us







0 comments: